Как строить график окружности по уравнению. Окружность на координатной плоскости. Преимущества построения графиков онлайн

Аналитическая геометрия дает единообразные приемы решения геометрических задач. Для этого все заданные и искомые точки и линии относят к одной системе координат.

В системе координат можно каждую точку охарактеризовать ее координатами, а каждую линию – уравнением с двумя неизвестными, графиком которого эта линия является. Таким образом геометрическая задача сводится к алгебраической, где хорошо отработаны все приемы вычислений.

Окружность есть геометрическое место точек с одним определенным свойством (каждая точка окружности равноудалена от одной точки, называется центром). Уравнение окружности должно отражать это свойство, удовлетворять этому условию.

Геометрическая интерпретация уравнения окружности – это линия окружности.

Если поместить окружность в систему координат, то все точки окружности удовлетворяют одному условию – расстояние от них до центра окружности должно быть одинаковым и равным окружности.

Окружность с центром в точке А и радиусом R поместим в координатную плоскость.

Если координаты центра (а;b) , а координаты любой точки окружности (х; у) , то уравнение окружности имеет вид:

Если квадрат радиуса окружности равен сумме квадратов разностей соответствующих координат любой точки окружности и ее центра, то это уравнение является уравнением окружности в плоской системе координат.

Если центр окружности совпадает с точкой начала координат, то квадрат радиуса окружности равен сумме квадратов координат любой точки окружности. В этом случае уравнение окружности принимает вид:

Следовательно, любая геометрическая фигура как геометрическое место точек определяется уравнением, связывающим координаты ее точек. И наоборот, уравнение, связывающее координаты х и у , определяют линию как геометрическое место точек плоскости, координаты которых удовлетворяют данному уравнению.

Примеры решения задач про уравнение окружности

Задача. Составить уравнение заданной окружности

Составьте уравнение окружности с центром в точке O (2;-3) и радиусом 4.

Решение .
Обратимся к формуле уравнения окружности:
R 2 = (x-a ) 2 + (y-b ) 2

Подставим значения в формулу.
Радиус окружности R = 4
Координаты центра окружности (в соответствии с условием)
a = 2
b = -3

Получаем:
(x - 2 ) 2 + (y - (-3 )) 2 = 4 2
или
(x - 2 ) 2 + (y + 3 ) 2 = 16 .

Задача. Принадлежит ли точка уравнению окружности

Проверить, принадлежит ли точка A(2;3) уравнению окружности (x - 2) 2 + (y + 3) 2 = 16 .

Решение .
Если точка принадлежит окружности, то ее координаты удовлетворяют уравнению окружности.
Чтобы проверить, принадлежит ли окружности точка с заданными координатами, подставим координаты точки в уравнение заданной окружности.

В уравнение (x - 2) 2 + (y + 3) 2 = 16
подставим, согласно условию, координаты точки А(2;3), то есть
x = 2
y = 3

Проверим истинность полученного равенства
(x - 2) 2 + (y + 3) 2 = 16
(2 - 2) 2 + (3 + 3) 2 = 16
0 + 36 = 16 равенство неверно

Таким образом, заданная точка не принадлежит заданному уравнению окружности.

Если расположить единичную числовую окружность на координатной плоскости, то для ее точек можно найти координаты. Числовую окружность располагают так, чтобы ее центр совпал с точкой начала координат плоскости, т. е. точкой O (0; 0).

Обычно на единичной числовой окружности отмечают точки соответствующие от начала отсчета на окружности

• четвертям - 0 или 2π, π/2, π, (2π)/3,
• серединам четвертей - π/4, (3π)/4, (5π)/4, (7π)/4,
• третям четвертей - π/6, π/3, (2π)/3, (5π)/6, (7π)/6, (4π)/3, (5π)/3, (11π)/6.

На координатной плоскости при указанном выше расположении на ней единичной окружности можно найти координаты, соответствующие этим точкам окружности.

Координаты концов четвертей найти очень легко. У точки 0 окружности координата x равна 1, а y равен 0. Можно обозначить так A (0) = A (1; 0).

Конец первой четверти будет располагаться на положительной полуоси ординат. Следовательно, B (π/2) = B (0; 1).

Конец второй четверти находится на отрицательной полуоси абсцисс: C (π) = C (-1; 0).

Конец третьей четверти: D ((2π)/3) = D (0; -1).

Но как найти координаты середин четвертей? Для этого строят прямоугольный треугольник. Его гипотенузой является отрезок от центра окружности (или начала координат) к точке середины четверти окружности. Это радиус окружности. Поскольку окружность единичная, то гипотенуза равна 1. Далее проводят перпендикуляр из точки окружности к любой оси. Пусть будет к оси x. Получается прямоугольный треугольник, длины катетов которого - это и есть координаты x и y точки окружности.

Четверть окружности составляет 90º. А половина четверти составляет 45º. Поскольку гипотенуза проведена к точке середины четверти, то угол между гипотенузой и катетом, выходящим из начала координат, равен 45º. Но сумма углов любого треугольника равна 180º. Следовательно, на угол между гипотенузой и другим катетом остается также 45º. Получается равнобедренный прямоугольный треугольник.

Из теоремы Пифагора получаем уравнение x 2 + y 2 = 1 2 . Поскольку x = y, а 1 2 = 1, то уравнение упрощается до x 2 + x 2 = 1. Решив его, получаем x = √½ = 1/√2 = √2/2.

Таким образом, координаты точки M 1 (π/4) = M 1 (√2/2; √2/2).

В координатах точек середин других четвертей будут меняться только знаки, а модули значений оставаться такими же, так как прямоугольный треугольник будет только переворачиваться. Получим:
M 2 ((3π)/4) = M 2 (-√2/2; √2/2)
M 3 ((5π)/4) = M 3 (-√2/2; -√2/2)
M 4 ((7π)/4) = M 4 (√2/2; -√2/2)

При определении координат третьих частей четвертей окружности также строят прямоугольный треугольник. Если брать точку π/6 и проводить перпендикуляр к оси x, то угол между гипотенузой и катетом, лежащим на оси x, составит 30º. Известно, что катет, лежащий против угла в 30º, равен половине гипотенузы. Значит, мы нашли координату y, она равна ½.

Зная длины гипотенузы и одного из катетов, по теореме Пифагора находим другой катет:
x 2 + (½) 2 = 1 2
x 2 = 1 - ¼ = ¾
x = √3/2

Таким образом T 1 (π/6) = T 1 (√3/2; ½).

Для точки второй трети первой четверти (π/3) перпендикуляр на ось лучше провести к оси y. Тогда угол при начале координат также будет 30º. Здесь уже координата x будет равна ½, а y соответственно √3/2: T 2 (π/3) = T 2 (½; √3/2).

Для других точек третей четвертей будут меняться знаки и порядок значений координат. Все точки, которые ближе расположены к оси x будут иметь по модулю значение координаты x, равное √3/2. Те точки, которые ближе к оси y, будут иметь по модулю значение y, равное √3/2.
T 3 ((2π)/3) = T 3 (-½; √3/2)
T 4 ((5π)/6) = T 4 (-√3/2; ½)
T 5 ((7π)/6) = T 5 (-√3/2; -½)
T 6 ((4π)/3) = T 6 (-½; -√3/2)
T 7 ((5π)/3) = T 7 (½; -√3/2)
T 8 ((11π)/6) = T 8 (√3/2; -½)

Окружностью называется множество точек плоскости, равноудаленных от данной точки, называемой центром.

Если точка С - центр окружности, R - ее радиус, а М - произвольная точка окружности, то по определению окружности

Равенство (1) есть уравнение окружности радиуса R с центром в точке С.

Пусть на плоскости задана прямоугольная декартова система координат (рис. 104) и точка С(а; b ) - центр окружности радиуса R. Пусть М(х; у ) - произвольная точка этой окружности.

Так как |СМ| = \(\sqrt{(x - a)^2 + (у - b)^2} \), то уравнение (1) можно записать так:

\(\sqrt{(x - a)^2 + (у - b)^2} \) = R

(x - a ) 2 + (у - b ) 2 = R 2 (2)

Уравнение (2) называют общим уравнением окружности или уравнением окружности радиуса R с центром в точке (а; b ). Например, уравнение

(x - l) 2 + (y + 3) 2 = 25

есть уравнение окружности радиуса R = 5 с центром в точке (1; -3).

Если центр окружности совпадает с началом координат, то уравнение (2) принимает вид

x 2 + у 2 = R 2 . (3)

Уравнение (3) называют каноническим уравнением окружности .

Задача 1. Написать уравнение окружности радиуса R = 7 с центром в начале координат.

Непосредственной подстановкой значения радиуса в уравнение (3) получим

x 2 + у 2 = 49.

Задача 2. Написать уравнение окружности радиуса R = 9 с центром в точке С(3; -6).

Подставив значение координат точки С и значение радиуса в формулу (2), получим

(х - 3) 2 + (у - (-6)) 2 = 81 или (х - 3) 2 + (у + 6) 2 = 81.

Задача 3. Найти центр и радиус окружности

(х + 3) 2 + (у -5) 2 =100.

Сравнивая данное уравнение с общим уравнением окружности (2), видим, что а = -3, b = 5, R = 10. Следовательно, С(-3; 5), R = 10.

Задача 4. Доказать, что уравнение

x 2 + у 2 + 4х - 2y - 4 = 0

является уравнением окружности. Найти ее центр и радиус.

Преобразуем левую часть данного уравнения:

x 2 + 4х + 4- 4 + у 2 - 2у +1-1-4 = 0

(х + 2) 2 + (у - 1) 2 = 9.

Это уравнение представляет собой уравнение окружности с центром в точке (-2; 1); радиус окружности равен 3.

Задача 5. Написать уравнение окружности с центром в точке С(-1; -1), касающейся прямой АВ, если A (2; -1), B(- 1; 3).

Напишем уравнение прямой АВ:

или 4х + 3y -5 = 0.

Так как окружность касается данной прямой, то радиус, проведенный в точку касания, перпендикулярен этой прямой. Для отыскания радиуса необходимо найти расстояние от точки С(-1; -1) - центра окружности до прямой 4х + 3y -5 = 0:

Напишем уравнение искомой окружности

(x +1) 2 + (y +1) 2 = 144 / 25

Пусть в прямоугольной системе координат дана окружность x 2 + у 2 = R 2 . Рассмотрим ее произвольную точку М(х; у ) (рис. 105).

Пусть радиус-вектор OM > точки М образует угол величины t с положительным направлением оси Ох , тогда абсцисса и ордината точки М изменяются в зависимости от t

(0 t х и у через t , находим

x = R cos t ; y = R sin t , 0 t

Уравнения (4) называются параметрическими уравнениями окружности с центром в начале координат .

Задача 6. Окружность задана уравнениями

x = \(\sqrt{3}\)cos t , y = \(\sqrt{3}\)sin t , 0 t

Записать каноническое уравнение этой окружности.

Из условия следует x 2 = 3 cos 2 t , у 2 = 3 sin 2 t . Складывая эти равенства почленно, получаем

x 2 + у 2 = 3(cos 2 t + sin 2 t )

или x 2 + у 2 = 3

Цель урока: ввести уравнение окружности, научить учащихся составлять уравнение окружности по готовому чертежу, строить окружность по заданному уравнению.

Оборудование : интерактивная доска.

План урока:

1. Организационный момент – 3 мин.
2. Повторение. Организация мыслительной деятельности – 7 мин.
3. Объяснение нового материала. Вывод уравнения окружности – 10 мин.
4. Закрепление изученного материала– 20 мин.
5. Итог урока – 5 мин.

Ход урока

2. Повторение:

− (Приложение1 Слайд 2 ) записать формулу нахождения координат середины отрезка;

− (Слайд 3) З аписать формулу расстояние между точками (длины отрезка).

3. Объяснение нового материала.

(Слайды 4 – 6) Дать определение уравнения окружности. Вывести уравнения окружности с центром в точке (а ;b ) и с центром в начале координат.

(х – а ) 2 + (у – b ) 2 = R 2 − уравнение окружности с центром С (а ;b ) , радиусом R , х и у – координаты произвольной точки окружности.

х 2 + у 2 = R 2 − уравнение окружности с центром в начале координат.

(Слайд 7)

Для того чтобы составить уравнение окружности, надо:

• знать координаты центра;
• знать длину радиуса;
• подставить координаты центра и длину радиуса в уравнение окружности.

4. Решение задач.

В задачах № 1 – № 6 составить уравнения окружности по готовым чертежам.

(Слайд 14)

№ 7. Заполнить таблицу.

(Слайд 15)

№ 8. Построить в тетради окружности, заданные уравнениями:

а) (х – 5) 2 + (у + 3) 2 = 36;
б ) (х + 1) 2 + (у – 7) 2 = 7 2 .

(Слайд 16)

№ 9. Найти координаты центра и длину радиуса, если АВ – диаметр окружности.

Дано:		Решение:
		R	Координаты центра
1	А (0 ; -6) В (0 ; 2)	АВ 2 = (0 – 0) 2 + (2 + 6) 2 ; АВ 2 = 64; АВ = 8 .	А (0; -6) В (0 ; 2) С (0 ; – 2) – центр
2	А (-2 ; 0) В (4 ; 0)	АВ 2 = (4 + 2) 2 + (0 + 0) 2 ; АВ 2 = 36; АВ = 6.	А (-2;0) В (4 ;0) С (1 ; 0) – центр

(Слайд 17)

№ 10. Составьте уравнение окружности с центром в начале координат, проходящей через точку К (-12;5).

Решение.

R 2 = ОК 2 = (0 + 12) 2 + (0 – 5) 2 = 144 + 25 = 169;
R = 13;

Уравнение окружности: х 2 + у 2 = 169.

(Слайд 18)

№ 11. Составьте уравнение окружности, проходящей через начало координат с центром в точке С (3; - 1).

Решение.

R 2 = ОС 2 = (3 – 0) 2 + (–1–0) 2 = 9 + 1 = 10;

Уравнение окружности: (х – 3) 2 + (у + 1) 2 = 10.

(Слайд 19)

№ 12. Составьте уравнение окружности с центром А (3;2), проходящей через В (7;5).

Решение.

1. Центр окружности – А (3;2);
2. R = АВ ;
АВ 2 = (7 – 3) 2 + (5 – 2) 2 = 25; АВ = 5;
3. Уравнение окружности (х – 3) 2 + (у − 2) 2 = 25.

(Слайд 20)

№ 13. Проверьте, лежат ли точки А (1; -1), В (0;8), С (-3; -1) на окружности, заданной уравнением (х + 3) 2 + (у − 4) 2 = 25.

Решение.

I . Подставим координаты точки А (1; -1) в уравнение окружности:

(1 + 3) 2 + (−1 − 4) 2 = 25;
4 2 + (−5) 2 = 25;
16 + 25 = 25;
41 = 25 – равенство неверно, значит А (1; -1) не лежит на окружности, заданной уравнением (х + 3) 2 + (у − 4) 2 = 25.

II . Подставим координаты точки В (0;8) в уравнение окружности:

(0 + 3) 2 + (8 − 4) 2 = 25;
3 2 + 4 2 = 25;
9 + 16 = 25;
В (0;8) лежит х + 3) 2 + (у − 4) 2 = 25.

III. Подставим координаты точки С (-3; -1) в уравнение окружности:

(−3 + 3) 2 + (−1− 4) 2 = 25;
0 2 + (−5) 2 = 25;
25 = 25 – равенство верно, значит С (-3; -1) лежит на окружности, заданной уравнением (х + 3) 2 + (у − 4) 2 = 25.

Итог урока.

1. Повторить: уравнение окружности, уравнение окружности с центром в начале координат.
2. (Слайд 21) Домашнее задание.

Определение 1 . Числовой осью (числовой прямой, координатной прямой ) Ox называют прямую линию, на которой точка O выбрана началом отсчёта (началом координат) (рис.1), направление

O → x

указано в качестве положительного направления и отмечен отрезок, длина которого принята за единицу длины .

Определение 2 . Отрезок, длина которого принята за единицу длины, называют масштабом .

Каждая точка числовой оси имеет координату , являющуюся вещественным числом. Координата точки O равна нулю. Координата произвольной точки A , лежащей на луче Ox , равна длине отрезка OA . Координата произвольной точки A числовой оси, не лежащей на луче Ox , отрицательна, а по абсолютной величине равна длине отрезка OA .

Определение 3 . Прямоугольной декартовой системой координат Oxy на плоскости называют две взаимно перпендикулярных числовых оси Ox и Oy с одинаковыми масштабами и общим началом отсчёта в точке O , причём таких, что поворот от луча Ox на угол 90° до луча Oy осуществляется в направлении против хода часовой стрелки (рис.2).

Замечание . Прямоугольную декартову систему координат Oxy , изображённую на рисунке 2, называют правой системой координат , в отличие от левых систем координат , в которых поворот луча Ox на угол 90° до луча Oy осуществляется в направлении по ходу часовой стрелки. В данном справочнике мы рассматриваем только правые системы координат , не оговаривая этого особо.

Если на плоскости ввести какую-нибудь систему прямоугольных декартовых координат Oxy , то каждая точка плоскости приобретёт две координаты – абсциссу и ординату , которые вычисляются следующим образом. Пусть A – произвольная точка плоскости. Опустим из точки A перпендикуляры AA 1 и AA 2 на прямые Ox и Oy соответственно (рис.3).

Определение 4 . Абсциссой точки A называют координату точки A 1 на числовой оси Ox , ординатой точки A называют координату точки A 2 на числовой оси Oy .

Обозначение . Координаты (абсциссу и ординату) точки A в прямоугольной декартовой системе координат Oxy (рис.4) принято обозначать A (x ; y ) или A = (x ; y ).

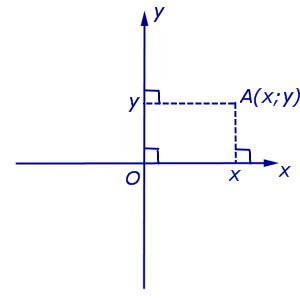
Замечание . Точка O , называемая началом координат , имеет координаты O (0 ; 0) .

Определение 5 . В прямоугольной декартовой системе координат Oxy числовую ось Ox называют осью абсцисс , а числовую ось Oy называют осью ординат (рис. 5).

Определение 6 . Каждая прямоугольная декартова система координат делит плоскость на 4 четверти (квадранта ), нумерация которых показана на рисунке 5.

Определение 7 . Плоскость, на которой задана прямоугольная декартова система координат, называют координатной плоскостью .

Замечание . Ось абсцисс задаётся на координатной плоскости уравнением y = 0 , ось ординат задаётся на координатной плоскости уравнением x = 0.

Утверждение 1 . Расстояние между двумя точками координатной плоскости

A 1 (x 1 ; y 1) и A 2 (x 2 ; y 2)

вычисляется по формуле

Доказательство . Рассмотрим рисунок 6.